Background
Is there any way of grounding our morality without arbitrarily assuming some primary value in the first place? I believe one way of doing so is to realize the following curious observation: by virtue of entering into an earnest dialogue which aims at uncovering some truth, both participants implicitly assume the constraints of the demands of rationality. This is an assumption all of us are taking for granted, explicitly or not. The cash value of this realization is that there are some principles of rationality that restrict which moral values we can coherently select. One principle of rationality I think might lead to a fruitful research project is what I call the principle of no self-defeaters. In other words, any set of moral values whose faithful practice leads to its own demise is a set of moral values we cannot rationally, and therefore, coherently hold. This is where I think computation may lend a helping hand to philosophers. Agent-based models have compared population sizes in a competitive resource scarce environment and have found altruism and egoism to lead to self-destructive populations; thus, I maintain, ruling them out as moral values. I would like to go a step further and simulate other, more complex moral systems in similar agent-based simulation environments to see if other popular moral theories are also self-defeating.
Simulating Moral Communities
Before I started this fellowship, I was all but certain of what the outcome of my research would be. I was wrong. But in order to understand how my prediction was wrong I should first explain the goal of the project.
In short, the goal of my research was to implement a proof of concept for a new methodology for doing moral philosophy, one that borrowed heavily from the field of complexity science. The idea was, if I could create a rudimentary (“agent-based”) simulation of social interactions (modeled as a prisoner’s dilemma exchange) within a population who all follow the same moral theory, then if that population self-destructs we could safely conclude (within the context of the simulation) that that particular moral theory was self-defeating.
More concretely, a prisoner’s dilemma is a scenario where two agents (or prisoners) can either “cooperate” or “defect” with one another. If one agent decides to cooperate, they will lose, say, +1 resource point (the more resources you have the higher the chance of reproducing). If that agent is lucky and their counterpart also cooperates, then they will gain +3 resources points. So if both parties cooperate, both parties walk away with +2 resource points (or a lower prison sentence, whichever you prefer). Crucially, however, each agent doesn’t know in advance what the other will do. Below is a visualization, called a “game theory matrix,” of how each possible scenario can play out in the more traditional scenario of two prisoners cooperating with or defecting from their partner in crime:
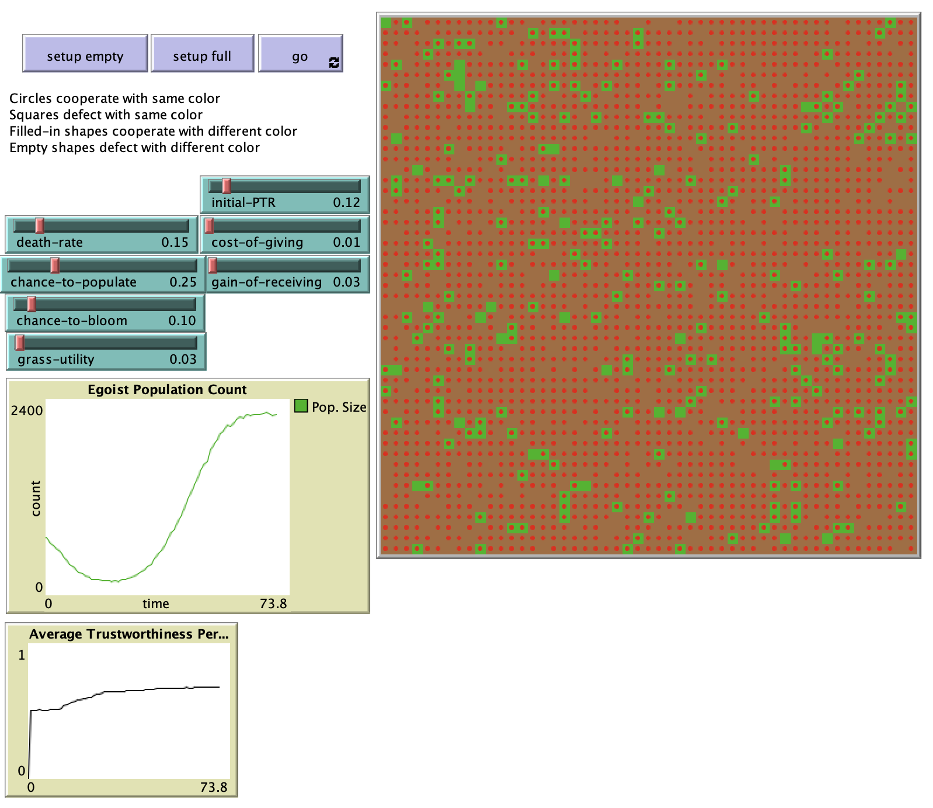
A snapshot of the simulation. Each red dot represents an agent, each red tile represents a resources tile that has been depleted, and each green tile represents a resource tile that is yet to be utilized. Resources affect energy, but not substantially. Their purpose is to introduce an extra degree of randomness into the simulation. Notice the two plots. The top one shows the initial decline and later recovery of the egoist population. The bottom one shows a steady increase of the average rate of trustworthiness. Both plots trend upwards over time.
The moral theory I wanted to focus on was what is sometimes called ethical egoism: an act is right if and only if it benefits me. I predicted that if any moral theory would fail to sustain a population of socially interacting agents, it would be this one. What I found was far more interesting.
